|
|
|
نوشته شده در شنبه 12 مرداد 1392
بازدید : 2329
نویسنده : امیر حسین دلشاد غلامی
|
|
امی های مختلف نیاز به تمرکز و دقت بالا دارد چرا که یک اشتباه می تواند کل کار را از بین ببرد. از اوریگامی گاهی می توان در راه های مختلفی نیز استفاده کرد که یکی از انها ایجاد اثرات هنری است.
گروه خواندنی های باشگاه خبرنگاران، اوریگامی که از یکی ازسنت های قدیمی ژاپنی است این روزها طرفدارانی جهانی دارد که باعث شده است شکل های جدید وارد دنیای اوریگامی شود و حتی برخی در این صنعت به پیشتازی برسند.
"یوهان شرفت" هنرمند هلندی یکی از پیشتازان نقاشی و اوریگامی در اروپا و تقریبا کل دنیا است. او به زیبایی می تواند اوریگامی پرندگان را بسازد و پس از آن با استفاده از رنگ های مختلف آن ها دقیق ا مانند نمونه های واقعی می کند. ا مانند نمونه های واقعی می کند.
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در پنج شنبه 26 ارديبهشت 1392
بازدید : 1024
نویسنده : امیر حسین دلشاد غلامی
|
|
ه تساوی زیر نگاه کنید :
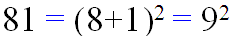
بله 81 برابر است با توان دوم ِ مجموع ارقامش.
آیا اعداد دیگری با این ویژگی وجود دارند؟
به عدد زیر نیز توجه کنید :

حتما ً شگفت زده شده اید !
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در پنج شنبه 26 ارديبهشت 1392
بازدید : 1105
نویسنده : امیر حسین دلشاد غلامی
|
|
سبت طلایی یکی از زیباییهای دنیای ریاضی است که رد آن را در جایجای طبیعت میتوان مشاهده کرد، از نسبت طول اندامهای انسان گرفته تا چشمنوازترین آثار معماری و حتی رشد مارپیچ دانههای گل آفتابگردان.
نسبت طلایی، عددی غیرگویا (گنگ) است که با حرف یونانی فی نمایش داده میشود. مقدار دقیق آن از رابطه 2/( 5√+1)= φ بدست میآید که حدود 1.618033988749894848294586834 است. بسیاری از هنرمندان معتقدند شکلهایی که در آنها نسبت طلایی رعایت شده است، چشمنوازترین شکلهای ممکن را تشکیل میدهند. مثال معروف آنها، کاغذهای استاندارد سری A (مانند کاغذ A4 به ابعاد 210×297 میلیمتر) است که در آنها نسبت طول به عرض برابر نسبت طلایی است. نسبت طلایی همچنین از رشته فیبوناچی نیز بدست میآید. رشته فیبوناچی یکی از جالبترین رشتههای اعداد است که در آن، عدد بعدی برابر حاصلجمع دو عدد قبلی است (1,1,2,3,5،8،13,21,34،55،89 و ...) و هرچه این رشته بیشتر ادامه پیدا کند، نسبت عدد بزرگتر به عدد قبلی به نسبت طلایی نزدیکتر میشود.
مایکل بلیک، موسیقیدانی که به ریاضیات علاقه دارد، قطعهای موسیقی را بر اساس نسبت طلایی نوشته است. او برای این کار، رقمهای اعشار نسبت طلایی را به صورت نتهای موسیقی بازنویسی کرده و حاصل آن را به صورت یک کلیپ ویدیویی آماده کرده است.
کلیپ ویدیویی را از اینجا دانلود کنید.
شما از شنیدن این موسیقی چه حسی پیدا می کنید؟
منبع:http://www.riazisara.ir
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در پنج شنبه 26 ارديبهشت 1392
بازدید : 1025
نویسنده : امیر حسین دلشاد غلامی
|
|
شگفتی های عدد هفت
*رنگین کمان 7 رنگ دارد .
*عجایب جهان 7 تا هستند .
* سوره حمد که اولین سوره قرآن است 7 آیه دارد .
* آسمان 7 طبقه دارد .
*موسیقی ایران و یونان 7 دستگاه دارد .
* 7 نوع ساز بادی وجود دارد .
* 7 نت موسیقی وجود دارد .
* ایرانیان برای اهورامزدا 7 صفت نیک بر می شمردند .
* سفره سال نو 7 س دارد .
* عرفای بزرگ برای عشق و وصال 7 مرحله طی می کنند .
* طواف نیز 7 بار است .
منبع:http://mathcity37.blogfa.com
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در پنج شنبه 26 ارديبهشت 1392
بازدید : 1110
نویسنده : امیر حسین دلشاد غلامی
|
|
محققان دانشگاه «اموري» پس از نزديک به يک قرن توانستهاند معمايي را که سرينيواسا رامانوجن، رياضيدان هندي در بستر مرگ مدعي شده بود که در رويا به وي الهام شده، حل کنند.
رامانوجن در سال 1920 در بستر مرگ در نامه اي به معلم خود، گادفري هارولد هاردي، رياضيدان انگليسي به ترسيم چندين تابع جديد رياضي به همراه توضيحاتي در مورد شيوه عملکرد آنها پرداخت که تا آن زمان ناشناخته بود.
اکنون محققان بعد از چندين دهه اعلام کرده اند که حق با اين رياضيدان بوده و اينکه اين فرمول ميتواند رفتار سياهچالهها را توضيح دهد.
رامانوجن که يک رياضيدان خودآموخته بود، در يک دهکده محلي در جنوب هند متولد شد و به قدري در مورد رياضي تفکر ميکرد که دو بار از دانشکده اخراج شد.
نامه اين رياضيدان محتوي چند تابع بوده که نسبت به توابع کنوني تتا يا شکلهاي مدولار متفاوت هستند با اينحال همچنان از آنها تقليد ميکند.
توابع به معادلاتي مانند موج سينوسي گفته ميشود که به شکل يک نمودار بر روي محور کشيده شده و با محاسبه هر ورودي يا ارزش انتخاب شده، يک نتيجه به دست آيد.
اين رياضيدان هندي حدس زده بود که شکلهاي مادولار تقليدي وي با شکلهاي مادولار رايج که پيشتر توسط کارل جاکوبي شناسايي شده بود، مطابقت دارد و اينکه نتيجه هر دو، خروجيهاي مشابه براي ريشههاي يک است.
رامانوجن تصور ميکرد که اين الگوها توسط يک خداي هندي بر وي الهام شده است با اين حال کسي در آن زمان نفهميد که وي به چه دست يافته است.
وي پيش از اينکه بتواند ظن خود را اثبات کند، درگذشت اما بيش از 90 سال پس از مرگ وي، محققان توانستند اثبات کنند که اين توابع در حقيقت از شکلهاي مادولار تقليد ميکنند اما خصوصيات توصيفکننده خود مانند ابرتقارن را به اشتراک نميگذارند.
توسعه اين توابع ميتواند به فيزيکدانان در محاسبه آنتروپي يا سطح اختلال سياهچالهها کمک کند.
اين يافتهها در آستانه صد و بيست و پنجمين سالگرد تولد رامانوجن در کنفرانس 125 رامانوجن در دانشگاه فلوريدا ارائه شده است.
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در پنج شنبه 26 ارديبهشت 1392
بازدید : 917
نویسنده : امیر حسین دلشاد غلامی
|
|
1)باقي مانده تقسيم هر عدد بر 2 يا 5 برابراست با باقي مانده تقسيم رقم سمت راست عدد بر 2 يا 5.
مثال :باقي مانده تقسيم عدد 7358 بر 5 برابر است با باقي مانده تقسيم عدد 8بر5 که برابر 3 ميگردد.
2)باقي مانده تقسيم هر عدد بر 3يا 9 با باقي مانده تقسيم مجموع ارقام عدد بر 3 يا 9 برابر ميباشد.
3)براي تعيين باقي مانده تقسيم هر عدد بر 11 کافي است ارقام عدد را از سمت راست به چپ بترتيب زوج وفرد نوشته و مجموع ارقام مکانهاي فرد رااز مجموع ارقام مکانهاي زوج کم کرده وباقي مانده عددحاصل رابر11 بدست مي آوريم که همان باقي مانده تقسيم عدداوليه بر11 ميباشد.
4) براي تعيين باقي مانده تقسيم هرعدد بر 7 يا 13 کافي است ارقام عدد رااز سمت راست به چپ سه رقم سه رقم جدا کرده و دسته هاي سه تايي را يکي درميان اضافه وکم کرده و باقي مانده تقسيم عدد حاصل رابر 7يا 13 بدست مي آوريم.
5)براي تعيين باقي مانده تقسيم هرعددبر 27 يا 37 کافي است ارقام عدد رااز سمت راست به چپ سه رقم سه رقم جداکرده و مجموع دسته هاي سه تايي رايافته وعدد حاصل رابر 27 يا 37 تقسيم مي کنيم وباقي مانده حاصل همان باقيمانده تقسيم عدد اوليه بر 27 يا 37 ميباشد.
6)عددي بر 4 بخش پذير است که مجموع 2 برابر رقم دهگان ورقم يکان عدد بر 4 بخش پذير باشد.
مثلا" :132 بر 4 بخش پذير ميباشدزيرا 8=2+3×2 بوده که بر 4 بخش پذير است.
7)عددي بر 8 بخش پذير است که مجموع چهار برابر رقم صدگان ودو برابر رقم دهگان ورقم يکان آن بر 8 بخش پذير باشد.
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در دو شنبه 23 بهمن 1391
بازدید : 831
نویسنده : امیر حسین دلشاد غلامی
|
|
من هم برايم بسيار جالب بود و دوست داشتم شما هم بدونيد.
عدد 373 همان عدد مورد نظر است . از هر طرف به آن نگاه كني عدد اول است. اگر يك رقم يك رقم در نظر بگيريم ،هر رقمي يك عدد اول است. و همينطور اگر دو رقم د و رقم در نظر بگيريم باز هم اعداد اول داريم. و خود عدد هم كه سه رقمي است نيز عددي اول است. پس به اين عدد ، عدد بسيار اول مي گوئيم .
جالب بود نه؟؟؟؟؟
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در سه شنبه 3 بهمن 1391
بازدید : 1626
نویسنده : امیر حسین دلشاد غلامی
|
|
-

عباس،فرزند علی و امّ البنین، در روز چهارم شعبان سال 26 هجری قمری در مدینه چشم به جهان گشود.مادرش فاطمه، دختر حزام بن خالد بود که نیاکانش همه از دلیر مردان عرب بوده
و در شجاعت و دلیری در دنیای عرب مشهور بوده اند.
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 1751
نویسنده : امیر حسین دلشاد غلامی
|
|
ابوریحان محمد بن احمد بیرونی از دانشمندان بزرگ ایران در عل
وم حكمت و اختر شناسی و ریاضیات و تاریخ و جغرافیا مقام شامخ داشته، در سال ۳۶۲ هجری قمری در حوالی خوارزم متولد شده و از این جهت به بیرونی یعنی خارج از خوارزم معروف شده.
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
ادبیات ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 1672
نویسنده : امیر حسین دلشاد غلامی
|
|
اعداد مثلثی
1، 3، 6، 10، 15، 21 و ... بنظر شما این اعداد چه ویژگی مشترکی دارند؟ اگر دست به قلم نشویم و شکل نکشیم و آزمایش نکنیم، فهمیدن ارتباط میان آنها کمی دشوار است. به این شکل دقت کنید مشکل شما حل خواهد شد. به اعداد موجود در این سری، اعداد مثلثی می گوییم.
1 = 1
3= 1+2
6= 1+2+3
10= 1+2+3+4
15= 1+2+3+4+5
21= 1+2+3+4+5+6
. . .
اما شکل اول یک ایده جدید به ما می دهد که می توانیم این اعداد را همانند پاراگراف بالا نیز تفسیر کنیم.
به بیان دیگر می توان گفت که هرعدد مثلثی تشکیل شده است از حاصل جمع یکسری از اعداد متولی طبیعی. به این معنی که اولین عدد مثلثی مساوی است با مجموع یک عدد از اعداد طبیعی، دومین معادل است با مجموع دو عدد از اعداد طبیعی، سومین معادل است با مجموع س عدد از اعداد طبیعی و ... و بالاخره n امین عدد مثلثی معادل است با مجموع n عدد از اعداد طبیعی که اگر ریاضیات دبیرستان را هنوز فراموش نکرده باشید بخاطر خواهید آورد که مقدار این عدد معادل n(n+1)/2 خواهد بود. (یک تصاعد ساده حسابی)
مجموع دو عدد مثلثی متوالی
اگر هر دو عدد پشت سرهم در سری اعداد مثلثی را با هم جمع کنیم حاصل جمع یک عدد مربع می شود. مثلا" 1+3=4 یا 3+6=9 یا 6+10=16 و ... البته دلیل آن ساده است به شکل دوم توجه کنید و ببینید که چگونه دو مثلث قرمز و سبز روی هم تشکیل یک مربع را می دهند. (سعی کنید با استدلال ریاضی هم این موضوع را ثابت کنید، ساده است از همان رابطه بالا استفاده کنید.)
مطلب اخیر اغلب بصورت قضیه "مربع هر عدد طبیعی برابر است با مجموع دو عدد مثلثی متوالی" نیز مطرح می شود.
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 1769
نویسنده : امیر حسین دلشاد غلامی
|
|
| |
نیکلای ایوانویچ لباچفسکی (Lobachevsky, Nikolay Ivanovich) از جمله اولین کسانی بود که قواعد هندسه اقلیدسی را که بیش از 2000 سال بر علوم مختلف ریاضی و فیزیک حاکم بود درهم شکست. کسی باورش نمی شد هنگامی که اروپا مرکز علم بود شخصی در گوشه ای از روسیه بتواند پایه های هندسه اقلیدسی را به لرزه در بیاورد و پایه های علم در قرن نوزدهم را پی ریزی کند.
خیال نداریم راجع به خود او صحبت کنیم بلکه می خواهیم بطور مختصر بیان کنیم که او چه کرد. در میان اصول هندسه اقلیدسی اصلی وجود دارد به اینصورت : از هر نقطه خارج یک خط نمی توان بیش از یک خط موازی ( در همان صفحه ای که خط و نقطه در آن قرار دارند) به موازات آن خط رسم کرد.
در طول سالها این اصل اقلیدس مشکل بزرگی برای ریاضی دانان بود. چرا که ظاهری شبیه به قضیه داشت تا اصل. مقایسه کنید آنرا با این اصل اقلیدس که می گوید بین هر دو نقطه می توان یک خط راست کشید و یا اینکه همه زوایای قائمه با هم برابر هستند.
حقیقت آن است که بسیاری از ریاضی دانان سعی کردند که این اصل اقلیدس را اثبات کنند اما متاسفانه هرگز این امر ممکن نشد. حتی خیام در برخی مقالات خود سعی در اثبات این اصل کرد اما او نیز همانند سایرین به نتیجه نرسید.
لباچفسکی (1792 - 1856) نیز همانند بسیاری از دانشمندان علوم ریاضی سعی در اثبات این اصل کرد و هنگامی که به نتیجه مطلوب نرسید نزد خود به این فکر فرو رفت که این چه هندسه ای است که بر پایه چنین اصل بی اعتباری استوار شده است. اما لباچفسکی در کوشش بعدی خود سعی کرد تا رابطه میان هندسه و دنیای واقعی را پیدا کند.
او معتقد بود اگر نتوانیم از سایر اصول هندسه اقلیدسی این اصل را ثابت کنیم باید به فکر مجموعه اصول دیگری برای هندسه باشیم. اصولی که در دنیای واقعی حضور دارند. او پس از بررسی های بسیار چنین بیان کرد :
از هر نقطه خارج یک خط می توان لااقل دو خط در همان صفحه به موازات خط رسم کرد
هر چند پس از این فرض بنظر می رسید که وی در ادامه به تناقض های بسیاری خواهد رسید اما او توانست بر اساس همین فرض و مفروضات قبلی اقلیدس به مجموعه جدید از اصول هندسی برسد که حاوی هیچگونه تناقضی نباشد. او پایه های هندسه ای را بنا نهاد که بعدها کمک بسیار زیادی به فیزیک و مکانیک غیر نیوتنی نمود.
|
:: موضوعات مرتبط:
ریاضی ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 1886
نویسنده : امیر حسین دلشاد غلامی
|
|
![]()
محمد بن حسن جهرودی طوسی مشهور به خواجه نصیرالدین طوسی در تاریخ 15 جمادی الاول 598 هجری قمری در طوس ولادت یافته است. او به تحصیل دانش علاقه زیادی داشت و از دوران کودکی جوانی در علوم ریاضی و نجوم و حکمت سرآمد شدو از دانشمندان معروف زمان خود گردید طوسی یکی از سرشناس ترین و با نفوذترین چهره های تاریخ فکری اسلامی است علوم دینی و علوم عملی را زیر نظر پدرش و منطق و حکمت طبیعی را نزد خالویش بابا افضل ایوبی کاشانی آموخت تحصیلاتش را در نیشابور به اتمام رسانید و در آنجا به عنوان دانشمندی برجسته شهرت یافت خواجه نصیرالدین طوسی را دسته ای از دانشوران خاتم فلاسفه ای و گروهی او را عقل حادی عشر(یازدهم) نام نهاده اند
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 2021
نویسنده : امیر حسین دلشاد غلامی
|
|
چهارضلعی یا چهاروَر به شکل مسطحی گفته میشود که از اتصال چهار نقطهٔ غیرهمخط در صفحه به وجود میآید. چهارضلعی دارای چهار ضلع و چهار زاویه است و مجموع زوایای داخلی آن ۳۶۰ درجهاست.
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 1718
نویسنده : امیر حسین دلشاد غلامی
|
|
پنج اصل متعارفی ، یا مفهوم عمومی اقلیدس
١_چیزهایی که با یک چیز مساوی اند ، با یکدیگر نیز مساوی اند
٢_اگر چیزهای مساوی به چیزهای مساوی اضافه شوند کلها مساوی اند
٣_اگر چیزهای مساوی از چیزهای مساوی کم شوند ، باقیمانده ها مساوی اند
۴_چیزهایی که بر یکدیگر منطبق شوند با یکدیگر مساوی اند
۵_کل از جزء بزرگتر است
و پنج اصل موضوع هندسی از اقلیدس
1
از هر نقطه میتوان خط مستقیمی به هر نقطۀ دیگر کشید
2-
هر خط مستقیم متناهی را می توان روی همان خط به طور نامحدود امتداد داد
3-
میتوان دایره ای با هر نقطۀ دلخواه به عنوان مرکز آن و با شعاعی مساوی هر پاره خط رسم شده از مرکز آن ترسیم کرد
4-
همۀ زوایای قائمه با هم مساوی اند
5-
اگر خط مستقیمی دو خط مستقیم را قطع کند به طوری که مجموع زاویای داخلی یک طرف آن کمتر از دو قائمه باشد این دو خط مستقیم اگر به طور نامحدود امتداد داده شوند ، در طرفی که دو زاویه مجموعا از دو قائمه کمترند ، همدیگر را قطع خواهند کرد
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 1829
نویسنده : امیر حسین دلشاد غلامی
|
|
بیوگرافی - زندگینامه دانشمندان - زندگینامه ارشمیدس
ارشميدس دانشمند و رياضيدان يونانی در سال 212 قبل از ميلاد در شهر سيراكوز يونان چشم به جهان گشود و در جوانی برای آموختن دانش به اسكندريه رفت. بيشتر دوران زندگيش را در زادگاهش گذرانيد و با فرمانروایاين شهر دوستی نزديك داشت. در اينجا سخن از معروفترين استحمامی است كه يك انسان در تاريخ بشريت انجام داده است. در داستانها چنين آمده است كه بيش از 2000 سال پيش در شهر سيراكوز پايتخت ايالت يونانیسيسيل آن زمان ارشميدس مكانيكدان و رياضيدان و مشاور دربار پادشاه يمرون يكیاز معروفترين كشفهای خود را در خزينه حمام انجام داد...
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 2226
نویسنده : امیر حسین دلشاد غلامی
|
|
بیوگرافی - زندگینامه دانشمندان - زندگینامه ارسطو
ارسطو در سال 384 پیش از میلاد در شهر استاگیرا مقدونیه که در 300 کیلومتری شمال آتن قرار دارد به دنیا آمد. پدر او دوست و پزشک پادشاه مقدونیه جد اسکندر مقدونی بود. ارسطو در جوانی برای تحصیل در آکادمی افلاطون راهی آتن شد. در آنجا توسط افلاطون عقل مجسم (Nous) آکادمی نام گرفت. وی پس از مرگ افلاطون آکادمی را ترک کرد و به آسیای صغیر رفت. در آنجا با دختر یک خانواده ثروتمند و پر نفوذ ازدواج کرد. بعد از مدت نه چندان طولانی فیلیپ پادشاه مقدونیه ارسطو را برای آموزش فرزندش اسکندر به دربار خود دعوت نمود. زمانی که ارسطو شروع به تربیت اسکندر کرد اسکندر 13 سال داشت. او حدود 12 سال به این کار مشغول بود...
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 3347
نویسنده : امیر حسین دلشاد غلامی
|
|
مثلث یعنی سه گوشه ، هر سطح سه گوشه ، سه کرده شده
در ریاضی
اگر سه نقطه غیر واقع بر یک خط راست را دو به دو به هم وصل کنیم شکلی بدست می آید که آن را مثلث می گویند
:: موضوعات مرتبط:
ریاضی ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 2197
نویسنده : امیر حسین دلشاد غلامی
|
|

شهرت علمی وی مربوط به کارهایی است که در ریاضیات مخصوصاً در رشته جبر انجام داده به طوری که هیچ یک از ریاضیدانان قرون وسطی مانند وی در فکر ریاضی تأثیر نداشته اند.
خوارزمی ابوجعفر محمدبن موسی از دانشمندان بزرگ ریاضی و نجوم می باشد.
: منبع:www.aftab.ir - آفتاب
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
ادبیات ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 2077
نویسنده : امیر حسین دلشاد غلامی
|
|
|
:: زندگي و مرگ خيام
آرامگاه خیام که در محله کهن شادیاخ در نیشابور است.عمر خیام در سده پنجم هجری در نیشابور زاده شد. فقه را در میانسالی در محضر امام موفق نیشابوری آموخت؛ حدیث، تفسیر، فلسفه، حکمت و اختر شناسی را فراگرفت. برخی نوشتهاند که او فلسفه را مستقیما از زبان یونانی فرا گرفته بود.
در حدود ۴۴۹ تحت حمایت و سرپرستی ابوطاهر، قاضیالقضات سمرقند، کتابی دربارهٔ معادلهای درجهٔ سوم به زبان عربی نوشت تحت نام رساله فی البراهین علی مسائل الجبر و المقابله نظام الملک طوسی رابطهای نیکو داشت، این کتاب را پس از نگارش به خواجه تقدیم کرد. پس از این دوران خیام به دعوت سلطان جلاالدین ملکشاه سلجوقی و وزیرش نظام الملک به اصفهان میرود تا سرپرستی رصدخانهٔ اصفهان را بهعهده گیرد. او هیجده سال در آنجا مقیم میشود. به مدیریت او زیج ملکشاهی تهیه میشود و در همین سالها (حدود ۴۵۸) طرح اصلاح تقویم را تنظیم میکند. تقویم جلالی را تدوین کرد که به نام جلال الدین ملکشاه شهرهاست، اما پس از مرگ ملکشاه کاربستی نیافت. در این دوران خیام بهعنوان اختربین در دربار خدمت میکرد هرچند به اختربینی اعتقادی نداشت.در همین سالها(۴۵۶) مهمترین و تاثیرگذارترین اثر ریاضی خود را با نام رساله فی شرح مااشکل من مصادرات اقلیدس را مینویسد و در آن خطوط موازی و نظریهٔ نسبتها را شرح میدهد. پس از درگذشت ملکشاه و کشته شدن نظامالملک، خیام مورد بیمهری قرار گرفت و
|
|

|
|
مقبره خيام - نيشابور
|
|
|
|
کمک مالی به رصدخانه قطع شد بعد از سال ۴۷۹ اصفهان را به قصد اقامت در مرو که به عنوان پایتخت جدید سلجوقیان انتخاب شده بود، ترک کرد. احتمالا در آنجا میزان الحکم و قسطاس المستقیم را نوشت. رسالهٔ مشکلات الحساب (مسائلی در حساب) احتمالا در همین سالها نوشته شده است.
خیام در زندگی زن نگرفت و همسر بر نگزید.
باغی که آرامگاه خیام در آن قرار دارد، تصویر از کنار آرامگاه امامزاده محروق گرفته شدهاست و در ورودی قدیمی این باغ در تصویر دیده میشود.مرگ خیام را میان سالهای ۵۱۷-۵۲۰ هجری میدانند که در نیشابور اتفاق افتاد. گروهی از تذکره نویسان نیز وفات او را ۶۱۵ نوشتهاند،اما پس از بررسیهای لازم مشخص گردیده که تاریخ وفات وی سال ۵۱۷ بودهاست .مقبرهٔ وی هم اکنون در شهر نیشابور،در باغی که آرامگاه امامزاده محروق در آن واقع میباشد، قرار گرفتهاست.
|
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
ادبیات ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 2113
نویسنده : امیر حسین دلشاد غلامی
|
|
پیش از کشف رساله خیام در جبر، شهرت او در مشرقزمین به واسطه اصلاحات سال و ماه ایرانی و در غرب به واسطه ترجمه رباعیاتش بوده است و تقریباً تا حدود قرن ۱۹ میلادی از تحقیقات جبری او اطلاعی در دست نبود. به همین دلیل کوششها و تحقیقات خیام در علم جبر تأثیر چندانی در بسط این علم نداشته است و در آن زمان اروپائیان در جبر به مرحلهای رسیده بودند که آشنایی با رسالههای خیام تنها از جنبه تاریخی برای آنها با اهمیت بوده است. قدیمیترین کتابی که از خیام اسمی به میان آورده و نویسندهٔ آن هم عصر خیام بوده، نظامی عروضی
:: موضوعات مرتبط:
ریاضی ,
تاریخ ,
زندگی نامه ,
,
نوشته شده در یک شنبه 17 دی 1391
بازدید : 1934
نویسنده : امیر حسین دلشاد غلامی
|
|
برای پیدا کردن زاویه بین عقربه ساعت شمار و دقیقه شمار از فرمول زیر استفاده میشود.اگر پس از محاسبه زاویه از 180 درجه بیشتر شد عدد حاصل رو از 360 کم کنید تا زاویه به دست باید.
زاویه بین دو عقربه برابر است با:
( 30*ساعت -5/5 *دقیقه)
مثلا برای ساعت 12:20 عدد 5/5 را در 20 و30را 12 ضرب کنید. و حاصل ضرب ها را از هم کم کنید.پاسخ زاویه بین عقربه ها میشه
توجه:فرمول را از سمت چپ بخوانید

برگرفته شده از وبلاگ دنیای ریاضی
:: موضوعات مرتبط:
ریاضی ,
,
|
|
|










